epilogue

On discovering the formula that provides the title to this book, Leonhard Euler declared “It was like looking at a proof that God exists.” The formula can be derived from De Moivre’s Theorem by using the constant in place of the variable x.

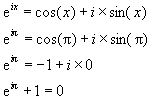
The result, which serves no practical purpose in mathematics, nevertheless connects in a succinct and direct relation “the five most important constants in mathematics ... [which] symbolize the four major branches of classical mathematics: arithmetic, represented by 0 and 1; algebra, by i; geometry, by pi; and analysis [calculus], by e” (Maor 160). Each of these branches of mathematics were considered separate disciplines, and the discovery of such an astonishing result showed the interconnectedness of all mathematics. The proof contains no theological elements, but the result appeals as mystic evidence.

The book Mathematics and the Imagination makes a grand claim for Euler’s result: “There is a famous formula - perhaps the most compact and famous of all formulas - developed by Euler from a discovery of De Moivre: . It appeals equally to the mystic, the scientist, the philosopher, the mathematician” (Kasner & Newman). Those 4 groups of people can make for strange bedfellows, and in this book they are joined by a fifth - a poet - where their interests intersect at this most unique formula that epitomizes all of mathematics.

The initial inspiration that lit this author’s lamp was born of a simple desire: to create a poem with a more strict -based constraint than Oulipian author Jacques Bens used in his 41 Sonnets Irrationels. Bens used the decimal expansion of to govern the number of lines per sonnet in his 41 sonnets. In order to create a more rigid constraint, I let the decimal expansion of govern the number of syllables in a line, and used the additional vocabulary constraint that every word had to contain the letter sequence “pi” in it.

Faced with a paucity of appropriate proper nouns, I relied on what the Oulipians call a deportmanteau word, which is a single word divided into constituent words through etymology, tmesis, or a more whimsical operation. In this way pithy became pi thy. Consequently, the structuring element of the text became the subject of the text itself: I was using to create formal constraints in an ode to .

The e poem is a univocal lipogram constructed using words containing the vowel e to the exclusion of all other vowels. Like the poem, each line of the e poem contains the same number of syllables as the decimal expansion of e. In addition, each line contains the same number of e’s as the decimal expansion of e. This restriction excludes words like “here”, “where”, and “there”, since they have more e’s than syllables.

The i poem for the imaginary constant is also a univocal lipogram. If the lines are numbered 1,2,3... each line n has one word, with the same number of i’s as the minimum power of i that equals iⁿ. This takes advantage of the cyclical exponentiation of i, which is demonstrated as follows:

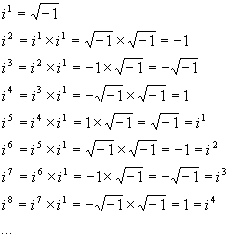
The powers of i only represent 4 unique numbers, and so the poem follows the exponentiation of i by cycling the number of i’s on each line through 1, 2, 3, 4, 1, 2, 3, 4 ...

Works Cited

Kasner, Edward, and James Newman. Mathematics and the Imagination. 1940.

Maor, Eli. e: the story of a number. Princeton: Princeton University Press, 1994.