When using computers as tools to understand language, Computer and Language Scientists have concerned themselves with two areas of study: natural language generation, and textual analysis. The former attempts to create programs capable of participating in meaningful linguistic interactions, while the latter attempts to use combinatoric and statistical tools to help better understand linguistic artifacts. The following study outlines and demonstrates a new method for textual analysis to add to the tools already available to the literary-minded computer scientist. The most successful area of computer-assissted textual analysis is the field of stylometry, which attempts to attribute texts to authors according to statistically quantified measures of style; the aim of the Finite State Poetry Machine (FSPM) is to provide a more general tool that allows us to analyse and compare features of poems without regard to their authors.

The Finite State Poetry Machine (FSPM) adapts the state-based or Moore Finite State Machine (FSM) to the analysis of poetry. An FSPM creates an abstraction of a poem by identifying a finite number of states, only one of which describes the current state of composition of the poem at any time.

In the first example of a poem in four letters (Figure 1a), the constituent letters
{ n , a , i , g }, correspond to the four main states of the FSPM:

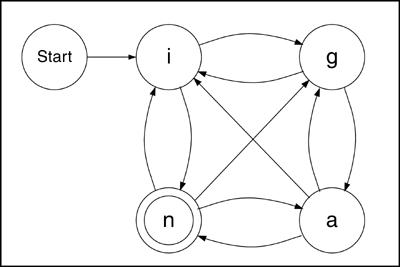
Figure 1a: poem

The number of states is known as the cardinality of the poem, commonly denoted by n. In the graphical representation of an FSPM each state is shown as an individual bubble. The following of one letter by another, or the transition between states, is represented by an arc between bubbles. The FSPM for the poem in Figure 1a, showing all states and transitions, is illustrated in Figure 1b.

Figure 1b: Finite State Poetry Machine

Aside from the main states of the poem, there are two additional special states: Start and End. The Start state is represented by the Start bubble, and the End state is shown by a double circle (in this instance around n). To see the FSPM in operation, start at the Start state, and trace through the poem following the transition arcs between states until the End state is reached.

To perform a quantitative analysis of a poem P using an FSPM, it is first necessary to construct a State-Transition Table. The table (Figure 1c), shows all of the states, and the number of transitions entering and leaving each state.

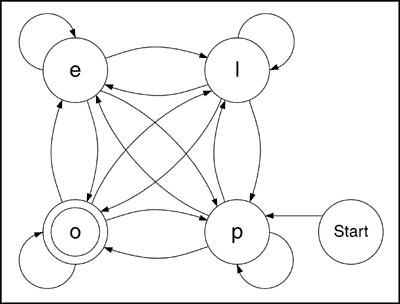
`Figure 1c: State-Transition Table

Note that the State-Transition Table in Figure 1c is symmetric, so the poem in Figure 1a is said to be a symmetric poem. All operations that can be performed on a symmetric matrix can be performed on a symmetric poem; hence there exists an inverse poem P^-1, which can be obtained by performing standard matrix operations on the State-Transition Table (the inverse poem is left as an exercise). Note that symmetry is a property unique to poems with cardinality n=4, since poems with cardinality n>4 or n<4 do not produce nxn State-Transition Tables.

A poem is said to be complete if each state has the maximum number of possible In's and Out's. For a complete poem with cardinality n=4, each entry in the In and Out columns is (n-1)=3. To obtain the sum of a poem P, commonly denoted by S (P), add the individual entries for the entire table (including Start and End). The sum of the poem in Figure 1a is S (P)=22. The sum of a complete poem P for n=4 is S (P)=24, or 2n(n-1)+2, which holds for the general case. If auto-transitions (transitions from state x to state x) are permitted, the sum of the poem can be up to S (P)=2n²+2. A complete auto-transitive poem is rare, especially if it contains u, i, or q states, since these states do not often appear in auto-transitions. John Riddell's "Pope Leo: El Elope: A Tragedy in Four Letters" is an example of a complete auto-transitive poem. We can see directly from the FSPM in Figure 2 that "Pope Leo: El Elope" is also a symmetrical poem.

Figure 2: FSPM for "Pope Leo: El Elope"

It can be easily shown through proof by contradiction that all complete poems with cardinality n=4, whether or not they are auto-transitive, are symmetrical. In general, for poems with small n, a greater sum results in a greater amount of alliteration, so the amount of alliteration a is directly proportional to the sum of the poem, or a~S (P).

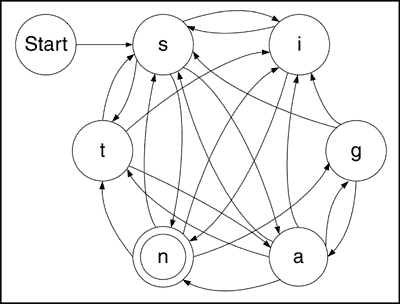
As the cardinality of a poem increases, the size and complexity of the FSPM increases. A poem in six letters is given in Figure 3a, with its corresponding FSPM in Figure 3b.

Figure 3a: poem

Figure 3b: FSPM for poem with cardinality n=6

Along with increased size and complexity in the poem, an increase in cardinality often (but not always) brings an increase in semantic coherence, denoted by c; hence n~c.

Since the study of Finite State Poetry Machines is so new, "Conclusions" is too strong a word to attach to the closing statements of this brief study; however, I will endeavour to make some general comments based on the preliminary research.

The first, and most subtle effect of the FSPM model is the foregrounding of the act of reading as travelling in space: your eye travels along the trajectories of letters across the page. The arrows between letters make the implied travel through and between words explicit. The FSPM’s graphical representation also allows us to see structural similarities between different poems in the relations of their constituent letters or states.

On a less heuristic level, an analysis of FSPMs can yield interesting properties– unavailable through traditional methods of analysis–like completeness, symmetry, and the hitherto undiscovered existence of the inverse poem, as well as the proportionality of attributes such as alliteration and semantic coherence.

Some of the limitations of FSPMs are inherent to the model itself. For one, an FSPM that specifies a poem does not necessarily uniquely specify it. Rather, in most cases (except for the trivial one where every instance of every letter in the poem is treated as a unique state, and the transitions follow the regular course of reading) the FSPM specifies a family of poems. This is not necessarily a limitation, since the generality of the FSPM is what allows us to draw the conclusions noted above. To reclaim a term for poetry that was stolen by Computer Science for programming languages from traditional grammar, FSPMs give us a way of specifying syntax.

Because FSPMs can grow quadratically as their cardinality increases (practice with FSPMs shows that there is usually an implied squared term in the sum) the complexity of the graphical representation increases proportionally. At a certain point, the usefulness of a graphical FSPM is suspect, as anyone who tries to draw an FSPM for a poem using all 26 letters will soon discover. The potential for discovery lies in the grounds for analysis of poems with large cardinality laid by the analysis of poems with smaller cardinality through an inductive process. The techniques developed in this paper, along with further techniques that are currently under consideration and those that remain to be discovered, can be implemented easily in any computer language supporting mapping Abstract Data Types. Once appropriate constants are discovered, the proportionalities can be defined as functions to obtain quantitative measurement systems.

The possibility of typing a poem into a computer and receiving a printed analysis of it is now within our grasp. Qualitative analysis of poetry can now be augmented by quantitative measurements made possible by a new intersection of Language and Computer Science: a digital scale to weigh the properties of poetics.

Since the Chomskian revolution, the study of Linguistics has seemed less a Humanity than a Mathematical Science. With the analytical tools developed in Computational Linguistics, the Humanities can now use computers to reclaim language for humanity. The possibilities, as always, are endless.